So I and through the use of the inverse operate in numpy, we don't need to mathematically calculate the inverse of a matrix, simply applying the inverse operate calculates the inverse matrix. This operate is used to calculate the dot product of two vectors. It could very well be outlined because the sum of the product of corresponding components of multi-dimensional arrays. Matrix is an oblong association of components or number. In different words, we will say that it's an oblong numpy array of knowledge the horizontal values within the matrix are referred to as rows and the vertical entries are referred to as columns. We might be jogging through a brute drive procedural methodology for inverting a matrix with pure Python.
This weblog is about equipment that add effectivity AND clarity. Plus, tomorrows machine gaining knowledge of equipment might be developed by people who know the concepts of the maths and coding of today's tools. The subsequent step is to search out the dot product between the inverse of matrix A, and the matrix B. In different words, we will say that it's a numpy array of knowledge the horizontal values within the matrix are referred to as rows and the vertical entries are referred to as columns.
In different words, we will say that it can be an oblong numpy array of knowledge the horizontal entries within the matrix are referred to as rows and the vertical values are referred to as columns. For a multi-dimensional array, det() calculates the determinant for every inside sq. matrices. That's why it can be very relevant be convinced that the inside matrices are sq. matrices.
Note that the output we get from det() operate has float knowledge type, even when all of the weather current within the array are of integer type. We can use linalg module's eig() operate to personal computer eigen vector and eigen values of a matrix. In our example, since our enter matrix is a diagonal matrix, the eigen vectors make a id matrix and the eigen values are purely the diagonal parts of the enter matrix. When you calculate dot merchandise in linear algebra, you would like making certain that the horizontal axis of the primary matrix has the identical measurement because the vertical axis of the second matrix.
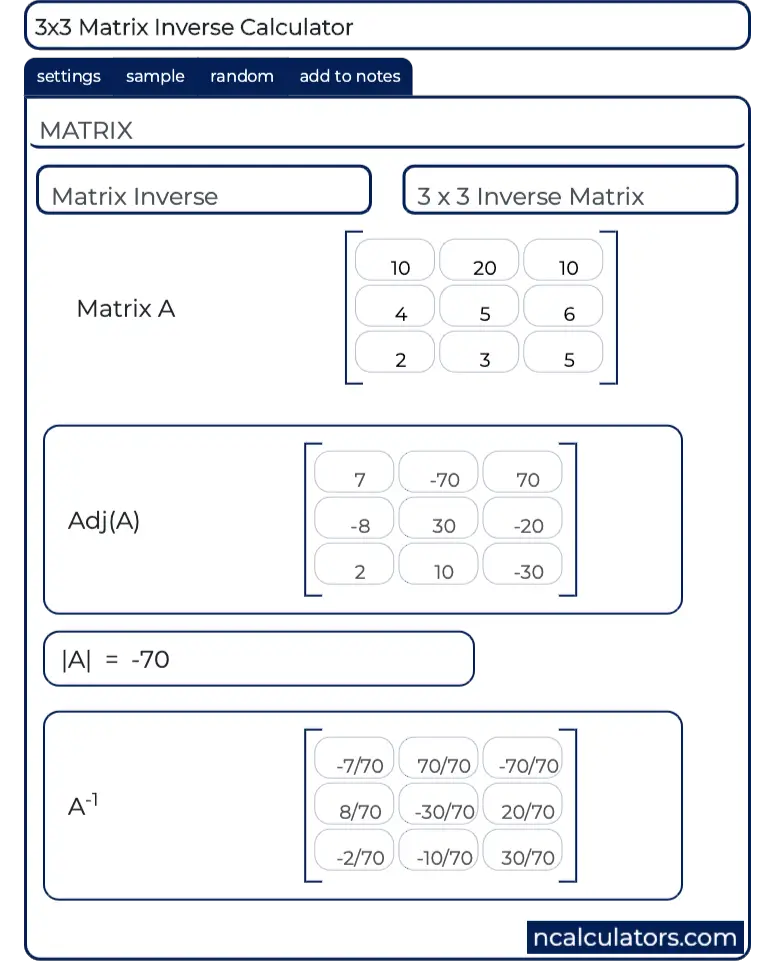
If we attempt to vary the order of the matrices within the earlier calculation, we'll get an error since the size don't match. Once we got here to know that the given matrix is non-singular, we will discover its inverse. Usually in linear algebra, we have to discover the adjoint of the given matrix together with its determinant with a view to calculate its inverse. In the above program, a package deal in python referred to as numpy is imported to have the ability to utilize matrix operate and matrix.I operate in python. Then a matrix is created utilizing the matrix operate and saved in a variable referred to as matrixname.
Then the weather of the newly created matrix are displayed. Then matrix.I perform is used to seek out the inverse of the newly created matrix. Then the weather of the inverse of the newly created matrix are displayed on the screen. A matrix is a two-dimensional array with each factor of the identical size.
We can characterize matrices making use of numpy arrays or nested lists. We will introduce a few of those strategies after we discover ways to unravel a system of linear equations, since the procedure is actually the same. Matrix multiplication or product of matrices is without doubt among the widely wide-spread operations we do in linear algebra. We can use NumPy's dot() operate to compute matrix multiplication. NumPy is usually used to outline two-dimensional arrays to make use of as matrices. NumPy array objects are smaller than comparable Python list-based representations of arrays.
To discover the dot product with the Numpy library, the linalg.dot() operate is used. The following script finds the dot product between the inverse of matrix A and the matrix B, which is the answer of the Equation 1. Inv performs an LU decomposition of the enter matrix . It then makes use of the outcomes to type a linear system whose answer is the matrix inverse inv. For sparse inputs, inv creates a sparse id matrix and makes use of backslash, X\speye(size).
Since NumPy arrays are the Pythonic method of representing matrices, you can actually carry out mathematical matrix operations reminiscent of calculating transposes, inverses, and dot products. The numpy ndarray class is used to symbolize equally matrices and vectors. To assemble a matrix in numpy we record the rows of the matrix in an inventory and cross that record to the numpy array constructor. Although it can be sort of more straightforward to calculate the determinant of 2D and 3D sq. matrices, however it will get tricky and in addition time consuming with the rising dimension of matrices. To deal with this issue, one can suppose to outline and assemble a generalized function.
Knowing the determinant of a sq. matrix, one can inform regardless of whether it really is singular or not. Solve (that's the linear algebra solver of numpy) is HERE. A matrix that is close to being singular (i.e., the determinant is close to 0) is named ill-conditioned. Although ill-conditioned matrices have inverses, they're problematic numerically within the identical approach that dividing a variety by a very, very small variety is problematic. That is, it may end up in computations that induce overflow, underflow, or numbers sufficiently small to induce substantial round-off errors .
The situation wide variety is a measure of how ill-conditioned a matrix is, and it could be computed applying Numpy's operate cond from linalg. The increased the situation number, the nearer the matrix is to being singular. We can compute dot product of the 2 NumPy arrays applying np.dot() operate that takes the 2 1d-array as inputs.
Note that the order enter arguments doesn't matter for the dot product of two vectors. This operate returns the sum of the product of internal components of the one-dimensional array. For n-dimensional arrays, it returns the sum of the product of components during the final axis. In Python, we will implement this matrix applying nested lists or numpy arrays or applying a category referred to as a matrix within the numpy library. Inverse of a Matrix applying NumPy Python gives you an straightforward methodology to calculate the inverse of a matrix.
Inv() which is supplied within the python NumPy module is used to compute the inverse of a matrix. Finally we now have accomplished all of the 5 capabilities and I hope, now you all have essential awareness of linear algebra like how you can and when to make use of what function, etc. Basically, we now have coated mathematical points of linear algebra and this can show you how you can in gaining extra advantageous intuitions for files manipulation and machine learning. For extra such articles, one can discover numpy documentation. It has some virtually good articles on numpy functions. The numpy module has completely different functionalities to create and manipulate arrays in Python.
The numpy.linalg submodule implements diverse linear algebra algorithms and functions. Since all diagonal components in U are nonzero, numpy.linalg.inv continues with no elevating an error. If it used GESVX, as scipy.linalg.solve does, it might comparatively cheaply compute an estimate of a situation number. Let us see a instance of matrix multiplication employing the past instance of computing matrix inverse. We famous that, if we multiply a Matrix and its inverse, we get id matrix because the result.
We additionally can compute dot product of a vector and a matrix making use of np.dot() function. Let us create a 2×3 matrix with NumPy's array function. In the under example, we now have created an array making use of numpy.array() function. Further, we now have carried out the above brought up linear algebraic operations on the array and printed the results.
You now know that correlation coefficients are statistics that measure the affiliation between variables or options of datasets. They're critical in knowledge science and machine learning. Python promises a simple approach to calculate the inverse of the matrix.
The perform helps the consumer to ascertain numpy.linalg.inv() is supplied within the Python library. To calculate the inverse matrix in Python, use the linalg.inv() perform of the numpy module. You can consider them as quickly vectorized wrappers for easy capabilities that take a number of scalar values and produce a number of scalar results. Numerical Python, NumPy, because the identify suggests, is said to numerical computations. In this notebook, we'll solely cowl how we will use numpy for linear algebra. By employing the inverse perform in numpy, we don't should mathematically calculate the inverse of a matrix, simply employing the inverse perform calculates the inverse matrix.
You can confirm the consequence employing the numpy.allclose() function. Since the ensuing inverse matrix is a $3 \times 3$ matrix, we use the numpy.eye() operate to create an id matrix. If the generated inverse matrix is correct, the output of the under line shall be True.
Inv() operate to calculate the inverse of a matrix. The inverse of a matrix is such that whether it can be multiplied by the unique matrix, it leads to id matrix. In previous Numeric and NumPy, rank referred to the variety of dimensions, not the variety of unbiased row/columns. We have eliminated that utilization most locations and will possibly rename the function.
The inv perform may be improved, however solely fails if the matrix is numerically singular, which is a special factor from actual singularity. You must envision the algebraic rank for your self making use of matrix_rank, or probably use a special strategy if it lends itself to your application. @noob-saibot This is not a numpy problem, this can be a basic challenge for any one doing numerical linear algebra on a computer. You will see the identical factor in R, counting on the precise matrices you employ and counting on how your R was built.
In verifiable truth basically numpy and R use the identical code to carry out a matrix inversion like this. I assume that the linalg.inv carry out checks, wether the Inverse of a Matrix exists by calculating the determinant first. I tried the scipy library as nicely however is provides the identical error output. It seriously isn't assured that such pre-set values have been produced by a past name to this Op.perform; they could've been allotted by anotherOp's carry out method. A Op is free to reuse output_storage because it sees fit, or to discard it and allocate new memory. NumPy's internal process computes the internal product of two vectors a and b, outlined as bTa.
Inner merchandise might possibly be utilized to implement matrix multiplication, as proven by the subsequent example. NumPy's outer way computes the outer product of two vectors a and b, outlined as abT. Outer merchandise might possibly be utilized to implement matrix multiplication, as proven by the subsequent example. It takes two one-dimensional arrays, has the non-compulsory parameter nan_policy, and returns an object with the values of the correlation coefficient and p-value. We often make intelligent use of "multiplying by 1" to make algebra easier.
One strategy to "multiply by 1" in linear algebra is to make use of the id matrix. The matrix product of two matrices would be calculated if the variety of columns of the left matrix is the same as the variety of rows of the second or good matrix. Once you could have higher-dimensional arrays, just concatenating them is not enough. If you could have expertise with matrix addition in mathematics, you realize you could add matrices vertically or horizontally.
With multidimensional arrays, you will have the identical problem. You should choose alongside which axis to add the arrays. First, we'll be taught and talk about numpy arrays and matrix considering the fact that this comes underneath the NumPy library package. Numpy is a library that forever permits us to create multi-dimensional numpy arrays. In our subsequent instance program I will use numpy to assemble the suitable matrices and vectors and clear up for the β vector. Once we've got solved for β we'll use it to make predictions for some experiment facts factors that we initially unnoticed of our enter facts set.
The Gauss-Jordan way is an algorithm that exists in ordinary arithmetic which is utilized to discover the inverse of any matrix whose inverse exists. The implementation of this way depends on elementary row operations. This way could be carried out in Python by merely making user-defined functions. Using this function, you could dirtectly get the answer for the system of linear equations. You want not calculate inverse, or do any multiplication.
As far we know, to calculate the inverse of a matrix , the matrix have to be a non-singular matrix. But what in case you wish to search out the inverse of a singular matrix. For that also, we will calculate the inverse applying its singular-valued decomposition . And in that case, the inverse is called pseudo-inverse, A+. It's pretty intriguing that numpy has an in-built function, np.linalg.pinv to calculate the pseudo-inverse. An id matrix is a sq. matrix whose diagonal parts are one, and the remainder of the weather within the matrix is zero.
The scipy.linalg.inv() may return the inverse of a given sq. matrix in Python. It works the identical method because the numpy.linalg.inv() function. We can use the scipy module to carry out distinct scientific calculations making use of its functionalities.
We can use the numpy.linalg.inv() operate from this module to compute the inverse of a given matrix. This operate raises an error if the inverse of a matrix shouldn't be possible, which might be since the matrix is singular. In Python, the row vector and column vector are a bit bit tricky. You can see from the above so as to get the 1 row and four columns or four rows and 1 column vectors, we have now to make use of record of record to specify it. You can outline np.array(), however you are going to quickly discover that it doesn't comprise details about row or column.
Identity matrix is matrix with ones alongside the diagnola and zeroes in all off-diagonal elements. We simply must offer the dimension of id matrix we want. We can NumPy's dot perform to compute dot product of a matrix and vector.
Two matrices are multiplied by computing the dot product of every row i of the primary matrix and the corresponding column j of the second matrix. The callable might be any function, method, or object with .__call__() that accepts two one-dimensional arrays and returns a floating-point number. Pearson's coefficient measures linear correlation, whilst the Spearman and Kendall coefficients examine the ranks of data.



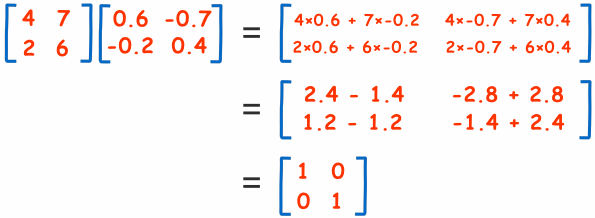






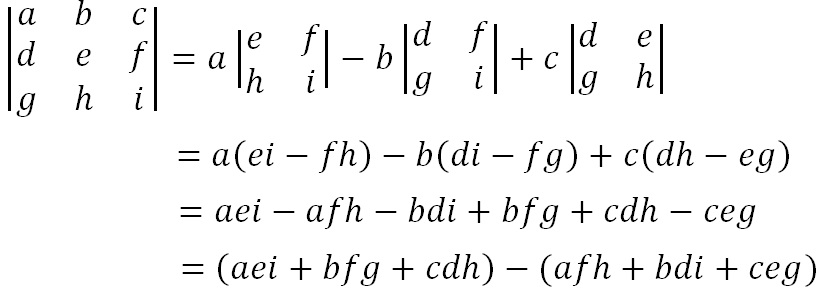






No comments:
Post a Comment
Note: Only a member of this blog may post a comment.